この記事を読むとわかること
メールマーケティングの売上向上の効果検証などビジネス上では様々なところで効果検証を行うことがありますが、効果検証を正しく行うことは非常に難しいです。 間違った効果検証を少しでも減らすために、この記事では効果検証をする際にどんなことに注意すればよいのか解説します。 今回の記事は因果グラフということで、効果検証をする際の便利な道具をご紹介します。
対象読者
- 効果検証したい/する必要がある、または興味がある
- 具体的にどのように効果検証すればいいのかわからない
- 効果検証をする際にどんなことに注意していいかわからない
因果グラフってなに?
効果検証をする際に、交換可能性を満たすために考慮すべき共変量は何なのか考える必要があります。 共変量を考慮すべきかどうか決めるために役に立つのが因果グラフです。 変数をノード、因果関係をエッジとしてグラフで変数間の因果関係を可視化します。
因果グラフを利用した共変量の選択
効果検証したい変数をY, Yに効果を与えるか検証したい変数をX、共変量をZとして基本的に以下の3つを意識すればよいです。
- 共変量ZがXとYの分岐点になる場合は、Zの影響を取り除く必要がある
- 共変量ZがXとYの合流点になる場合は、Zの影響を取り除いてはいけない
- 共変量ZがXとYの中間点になる場合は、Zの影響を取り除いてはいけない
上記3つ以外の場合は共変量Zを取り除く必要はなく、Zの影響を取り除いてはいけないこともないため、Zを無視してしまってよいです。
1.共変量Zが分岐点になる場合
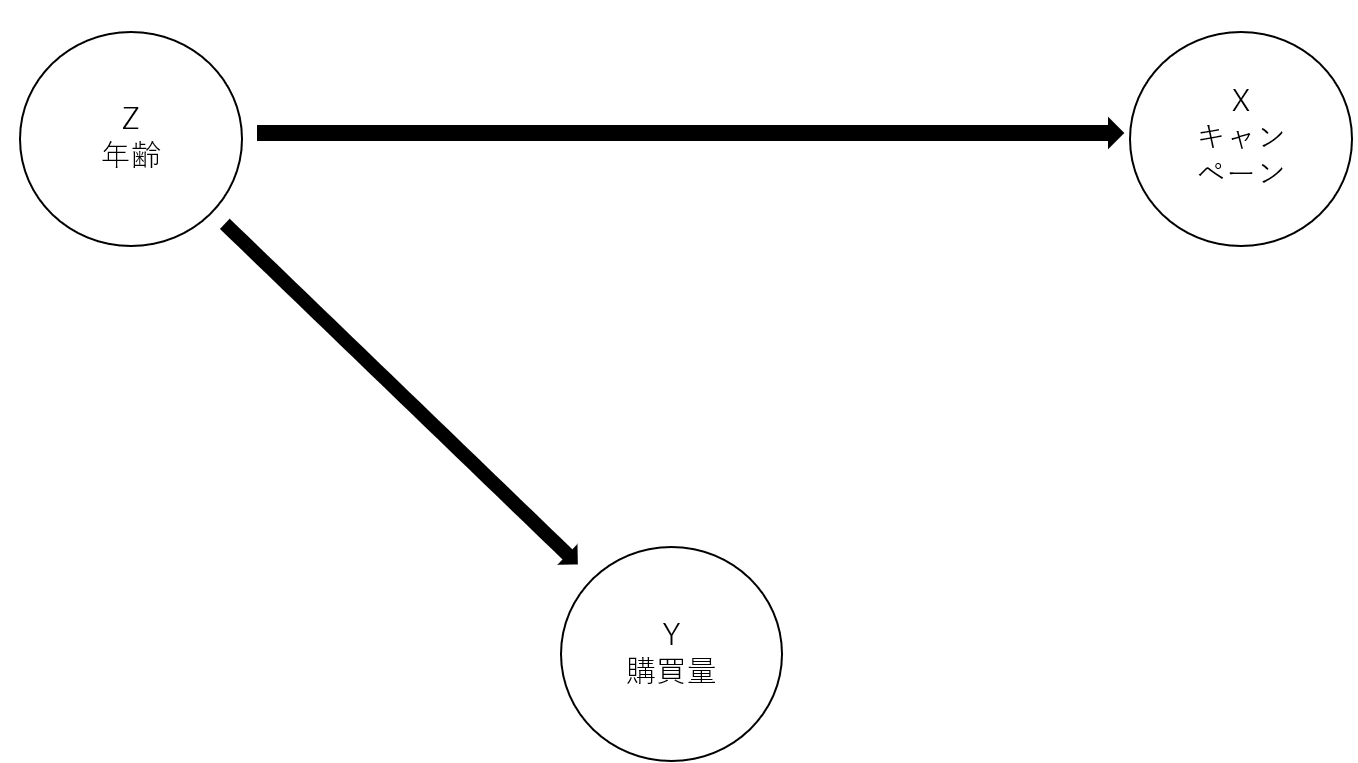
とある企業の商品は年齢が若い人ほど、購買量が多いとします。 そこで商品のキャンペーンを若い人に優先的に行い、商品の売上が増加したか見たいとします。 この場合の因果グラフは以下のようになっています。
このように共変量Zが分岐点となっている場合、Zの影響を取り除く必要があり、例では、年齢の影響を取り除く必要があります。 なぜかというと、年齢の若い人ほどもともと購買量が多いため、キャンペーンの効果で購入したからなのかもともと購入量が多いからなのかわからなくなるためです。
2.共変量Zが合流点になる場合
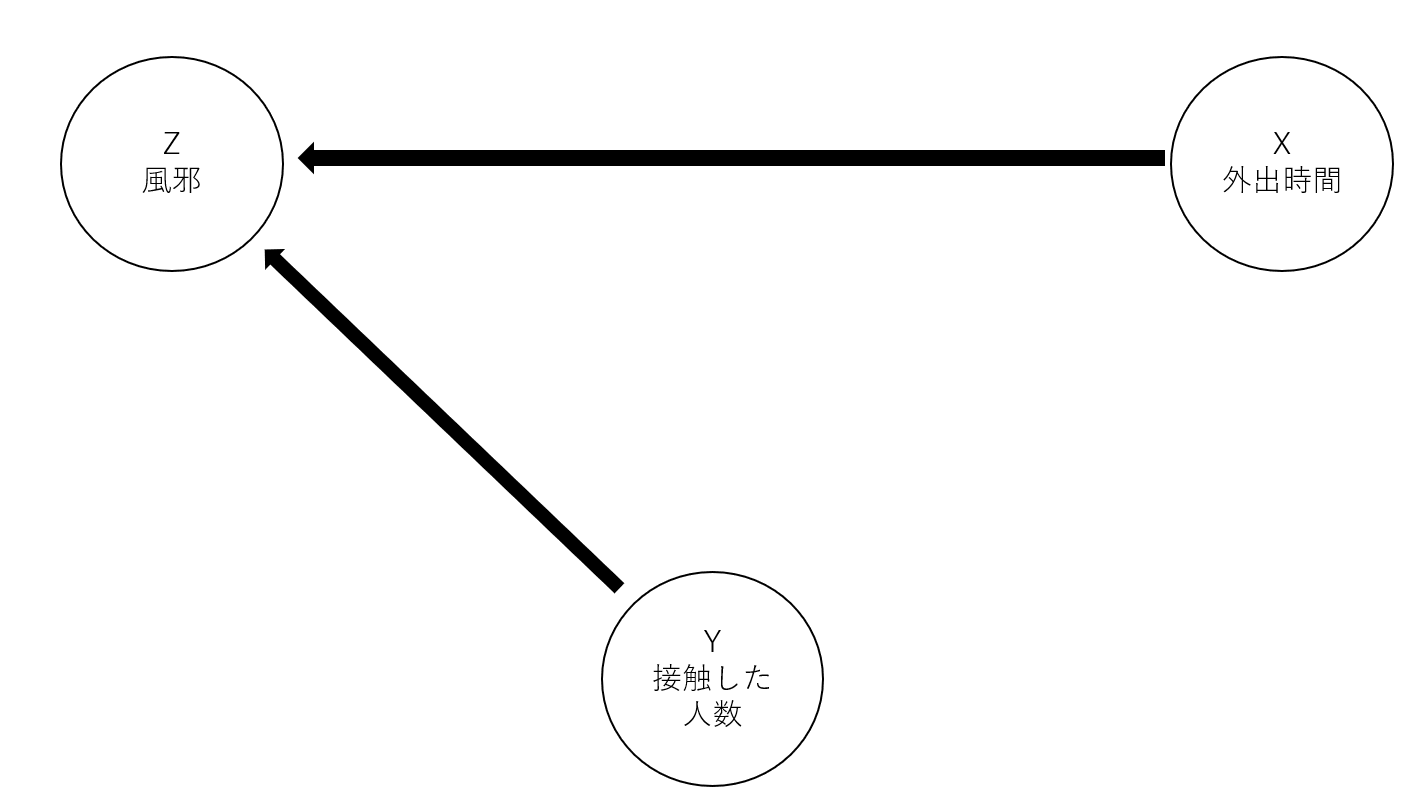
冬に風邪を引くかどうかは、寒い空間に滞在した時間と接触した人数で決まるとします。 そこで、寒い時間に滞在した時間と接触した人数には関係があるのか見たいとします。 この場合の因果グラフは以下のようになっています。
このように共変量Zが合流点となっている場合、Zの影響を取り除いてはいけません。 逆に取り除いてしまうと問題が生じます。 本質的に寒い空間に滞在した時間と接触した人数には関係がないはずです。 しかし風邪を引いた人に絞って見てみると、寒い空間に滞在した時間は長いが接触した人数は少ない人がでてきます(逆もしかり)。 つまり見かけ上寒い空間に滞在した時間と接触した人数に負の関係が生じます。 風邪を引いていない人に絞らず全体を見ると、寒い空間に滞在した時間は長く接触した人数は多い人や寒い空間に滞在した時間は短く接触した人数は少ない人がいるため、負の関係がなくなります。
3.共変量Zが中間点になる場合
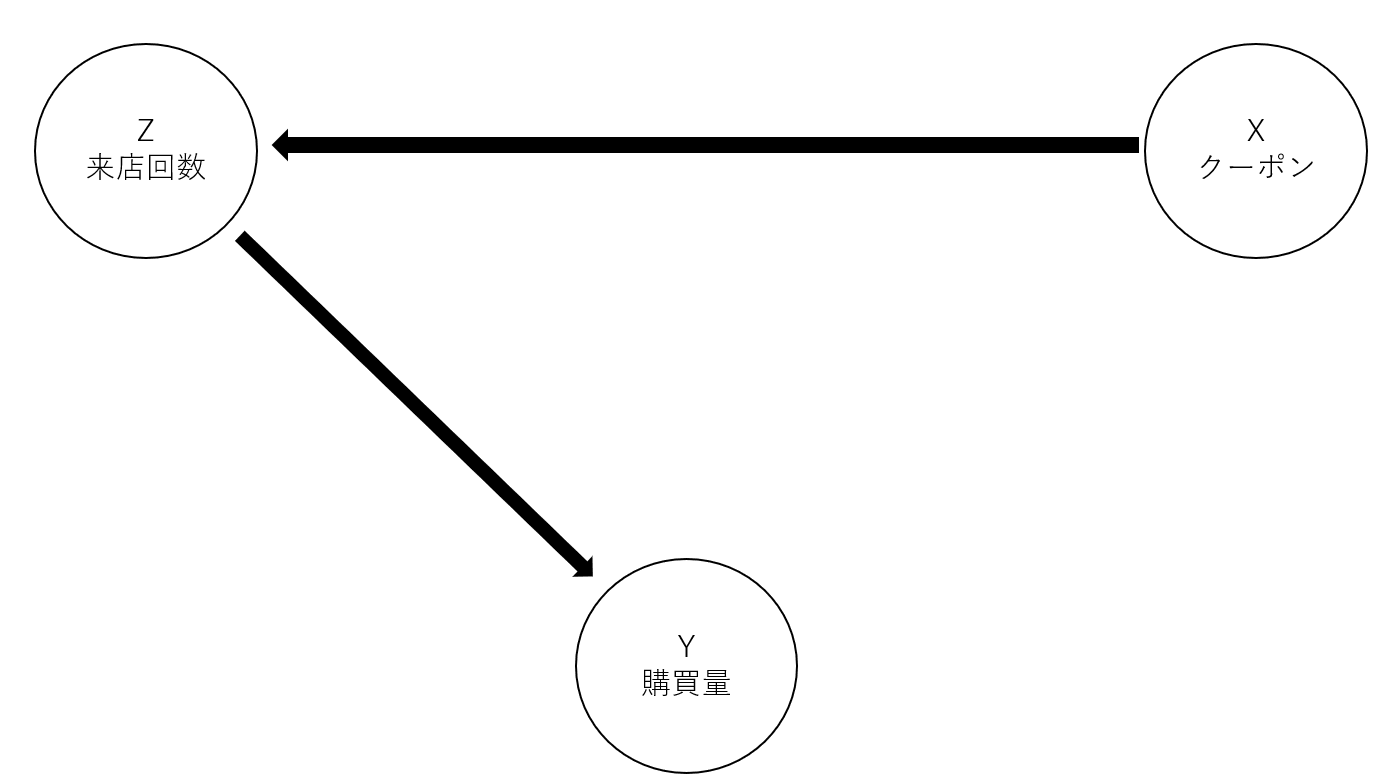
とある企業では顧客に定期的にクーポンを送っており、クーポンを送った人ほど来店回数が多くなり、購買量も多くなるとします。 クーポンの影響で購買量がどれだけ増加するのか検証したいとします。 この場合の因果グラフは以下のようになっています。
このように共変量Zが中間点となっている場合、Zの影響を取り除いてはいけません。 逆に取り除いてしまうと問題が生じます。 購買量におけるクーポンの影響を見ると、購買量は来店回数に依存するため、来店回数が同じような人で絞って来店回数を固定することで購買量の変動が少なくなってしまいます。 つまり、中間点である来店回数を考慮することで本来クーポンが購買量に与える影響が小さくなってしまう可能性があります。 こういった場合は来店回数を無視して、単純にクーポンを送ったかどうかと購買量の関係を見ればよいです。
まとめ
- 因果グラフを描いて変数間の関係を可視化することで、共変量の影響を消すべきか消さないべきかの判断が容易になる
- 共変量の影響を消すべきときと消すべきでないときがあるため、なんでもかんでも共変量を追加してはいけない
最後に
この記事では効果検証ををする際の因果グラフについて解説しました。 ここで解説した以外の観点でも気を付ける点はありますが、より詳細が知りたい方は効果検証についての本や記事などをご参照ください。 少しでも効果検証をする際の手助けになれば幸いです。
AITC
AIコンサルティンググループ
小川裕也